데이터 베이스 요약 - 7. 릴레이션 정규화
7. 릴레이션 정규화
부주의한 데이터베이스 설계는 데이터 중복을 야기하여 여러 가지 갱신 이상(update anomaly)을 유발함
정규화(normalization)는 주어진 릴레이션 스키마를 함수적 종속성과 기본 키를 기반으로 분석하여, 원래의 릴레이션을 분해함으로써 중복과 세 가지 갱신 이상을 최소화함.
7.1. 정규화 개요
세 가지 갱신 이상이 있다.
- 수정 이상(modification anomaly): 반복된 데이터 중에 일부만 수정하면 데이터의 불일치가 발생
- 삽입 이상(insertion anomaly): 불필요한 정보를 함께 저장하지 않고는 어떤 정보를 저장하는 것이 불가능
- 삭제 이상(deletion anomaly): 유용한 정보를 함께 삭제하지 않고는 어떤 정보를 삭제하는 것이 불가능
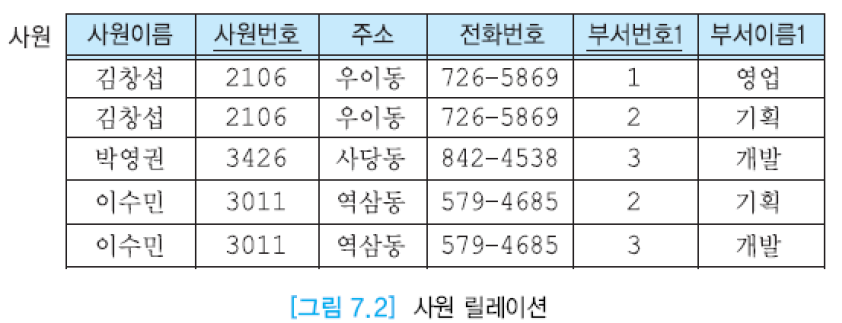
위 테이블을 다음과 같은 문제점이 있음.
(1) 정보의 중복: 각 사원이 속한 부서 수만큼 동일한 사원의 투플들이 존재하므로, 사원이름, 주소 등이 중복되어 저장 공간이 낭비됨.
(2) 수정 이상: 어떤 부서의 이름이 바뀔 때, 이 부서에 근무하는 일부 사원 투플에서만 부서이름을 변경하면 데이터베이스가 불일치 상태에 빠짐.
(3) 삽입 이상: 어떤 부서를 신설했는데, 아직 사원을 한 명도 배정하지 않았다면 이 부서에 관한 정보를 입력할 수 없음.
(4) 삭제 이상: 어떤 부서에 속한 사원이 단 한 명이 있는데, 이 사원에 관한 투플을 삭제하면 이 사원이 속한 부서에 관한 정보도 릴레이션에서 삭제됨.
정규형(normal form)의 종류.
제1 정규형(first normal form), 제2 정규형(second normal form), 제3 정규형(third normal form), BCNF(Boyce-Codd normal form), 제4 정규형(fourth normal form), 제5 정규형(fifth normal form)
일반적으로 데이터베이스 응용에서 데이터베이스를 설계할 때 BCNF까지만 고려함.
7.2. 함수적 종속성
함수적 종속성은 릴레이션의 애트리뷰트들의 의미로부터 결정되고, 제 2정규형부터 BCNF까지 적용됨.
릴레이션 스키마에 대한 주장이지, 릴레이션의 특정 인스턴스에 대한 주장이 아님. 릴레이션의 모든 인스턴스들이 만족해야 함.
어떤 애트리뷰트의 값은 다른 애트리뷰트의 값을 고유하게 결정할 수 있음. 그림 7.4의 사원 릴레이션에서 사원번호는 사원이름을 고유하게 결정함. 결정자(determinant)는 주어진 릴레이션에서 다른 애트리뷰트들을 고유하게 결정하는 하나 이상의 애트리뷰트. 결정자를 아래와 같이 표기하고, 이를 “A가 B를 결정한다” (또는 “A는 B의 결정자이다”)라고 말함.
A → B
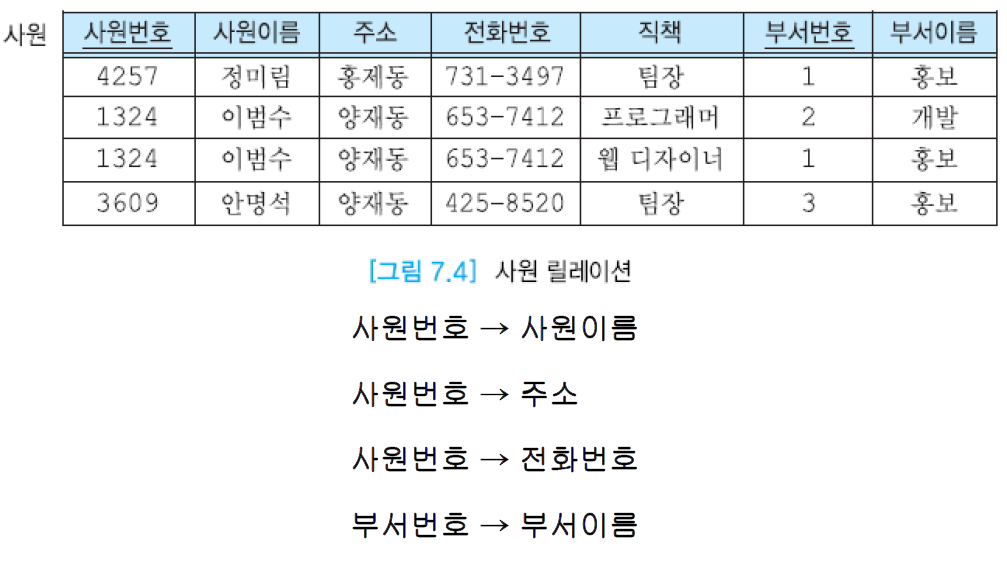
애트리뷰트 A가 애트리뷰트 B의 결정자이면 B가 A에 함수적으로 종속한다고 말함. 즉, 각 A값에 대해 반드시 한 개의 B값이 대응된다는 것.
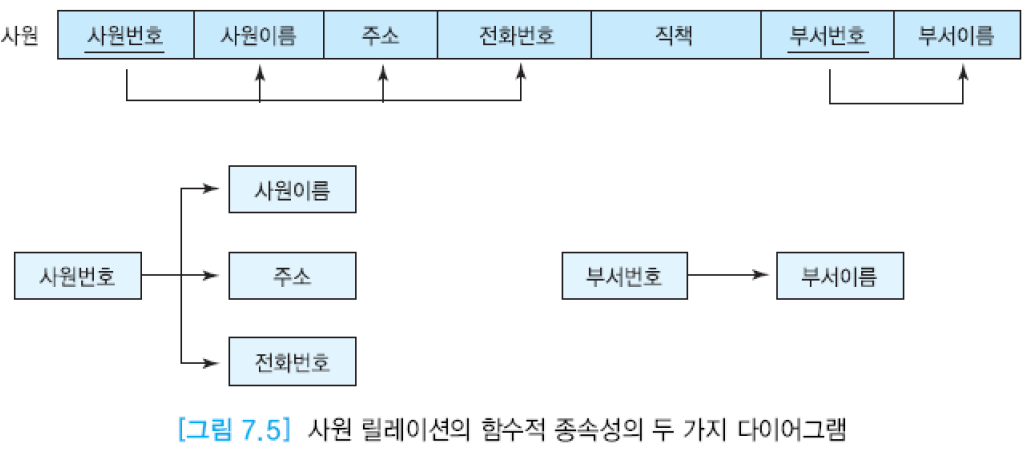
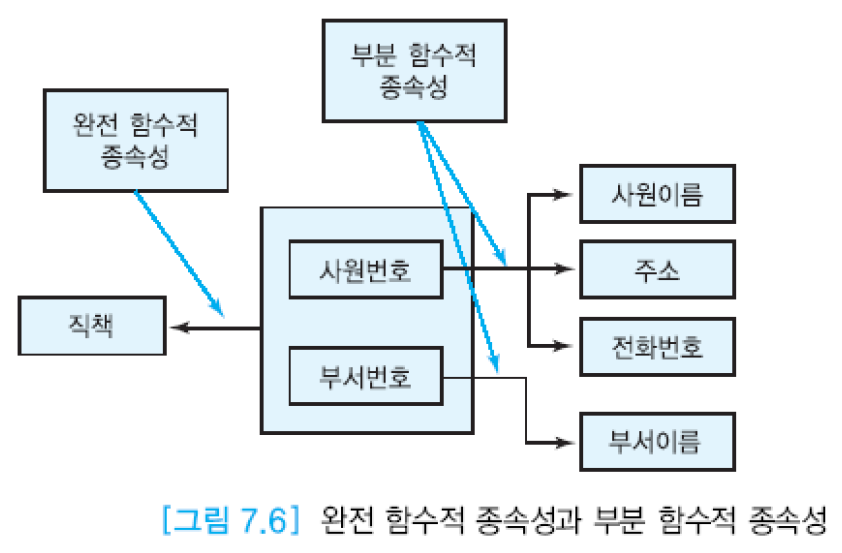
완전 함수적 종속성(FFD: Full Functional Dependency).
애트리뷰트 B가 애트리뷰트 A에 함수적으로 종속하면서 애트리뷰트 A의 어떠한 진부분 집합에도 함수적으로 종속하지 않으면, 애트리뷰트 B가 애트리뷰트 A에 완전하게 함수적으로 종속한다고 말함.
애트리뷰트 A는 복합 애트리뷰트.
이행적함수적종속성(transitive FD).
애트리뷰트 A, B, C가 있을 때, 애트리뷰트 C가 이행적으로 A에 종속한다(A→C)는 것의 필요 충분 조건은
A→B ∧ B→C
7.3. 릴레이션 분해
하나의 릴레이션을 두 개 이상의 릴레이션으로 나누는 것. 릴레이션 분해는 릴레이션에 존재하는 함수적 종속성에 관한 지식을 기반으로 함.
릴레이션을 분해하면 중복이 감소되고, 갱신 이상이 줄어드는 장점이 있는 반면에, 몇 가지 문제들을 야기할 수 있음.
- 분해되기 전에는 조인이 필요 없는 질의가 분해 후에는 조인을 필요로 하는 질의로 바뀔 수 있음
- 분해된 릴레이션들을 사용하여 원래 릴레이션을 재구성하지 못할 수 있음
무손실 분해(lossless decomposition)이란 분해된 두 릴레이션을 조인하면 원래의 릴레이션에 있는 정보를 완전하게 얻을 수 있다는 것.
손실이란 정보의 손실을 뜻함. 손실은 릴레이션을 분해한 후에 재구성 했을 때, 원래의 릴레이션에 있는 정보보다 적거나 많은 것.
7.4. 제1 정규형, 제2 정규형, 제3 정규형, BCNF
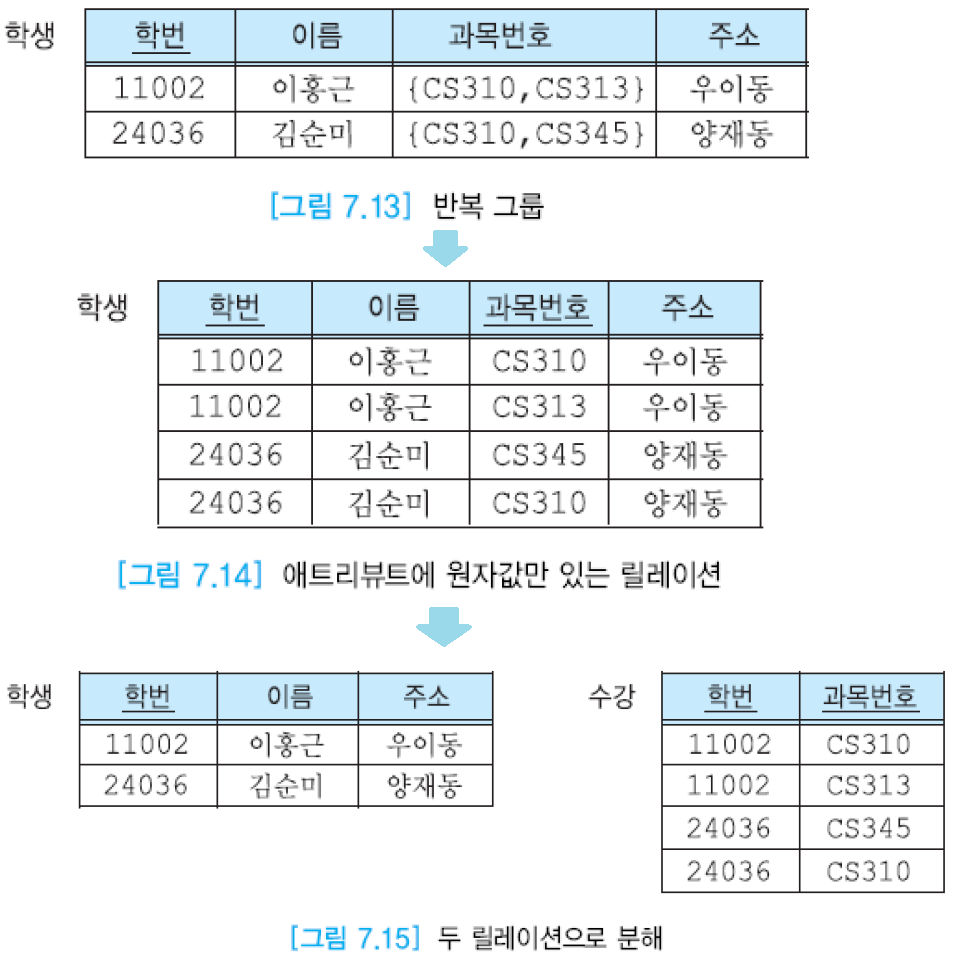
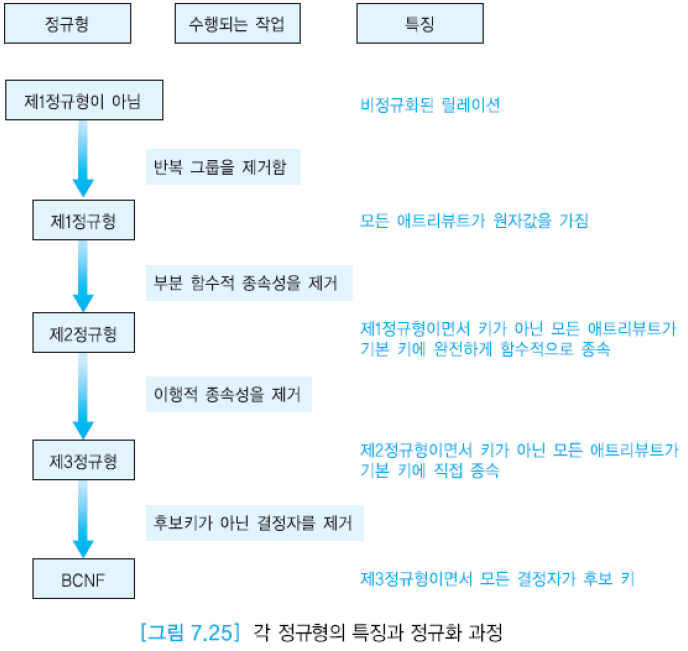
제1 정규형을 만족할 필요 충분 조건은 모든 애트리뷰트가 원자값만을 갖는다는 것. 즉, 모든 애트리뷰트에 반복 그룹(repeating group)이 나타나지 않는 것.
반복 그룹을 가진 릴레이션은 제1 정규형으로 바꿔야 함.
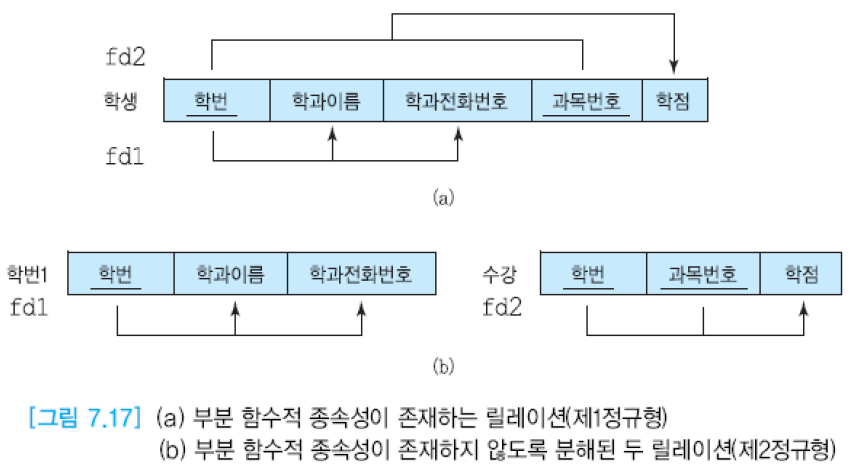
제2 정규형을 만족할 필요 충분 조건은 제1 정규형을 만족하면서, 후보 키에 속하지 않는 애트리뷰트들이 기본 키에 완전하게 함수적으로 종속하는 것.
기본 키가 두 개 이상의 애트리뷰트로 구성되었을 경우에만 제1 정규형이 제2 정규형을 만족하는가를 고려할 필요가 있음.
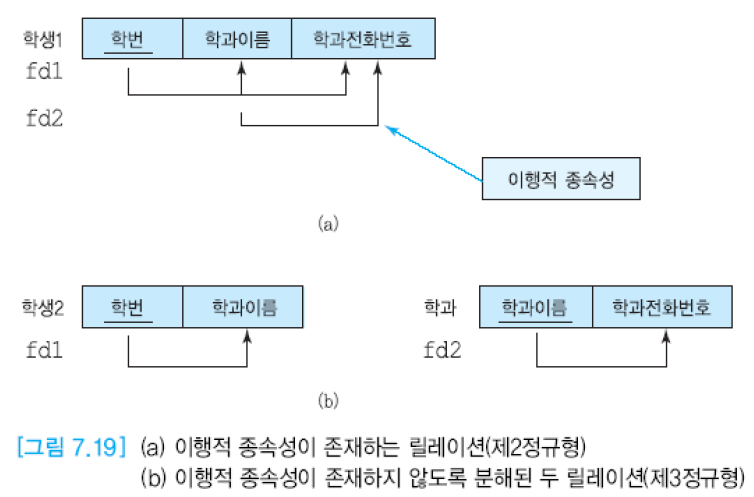
제3 정규형을 만족할 필요 충분 조건은 제2 정규형을 만족하면서, 키가 아닌 애트리뷰트가 기본 키에 이행적으로 종속하지 않는 것.
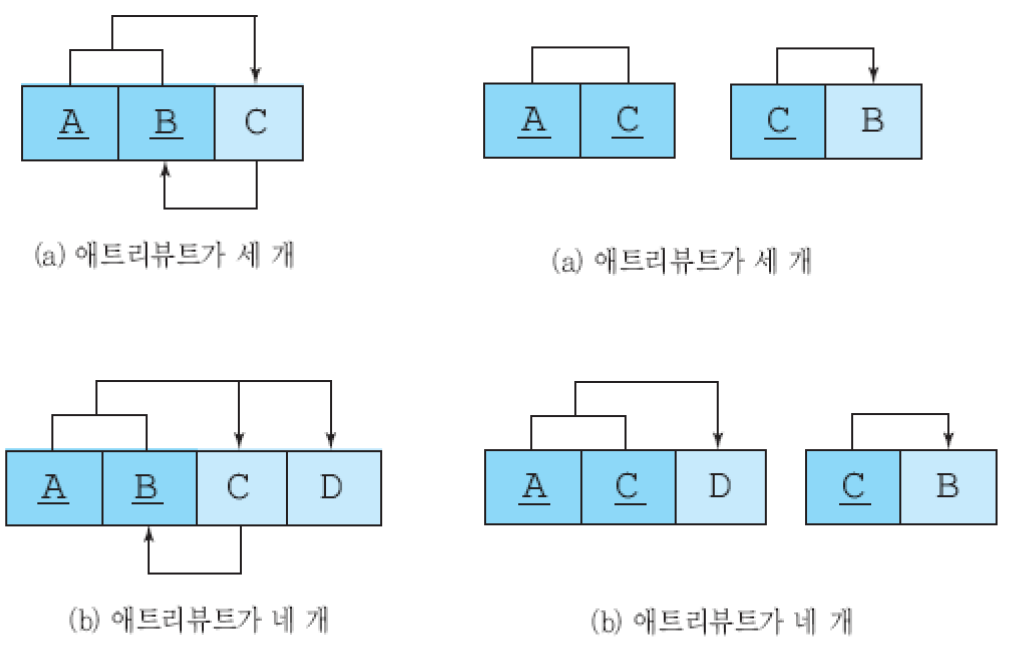
BCNF를 만족할 필요 충분 조건은 제3 정규형을 만족하고, 모든 결정자가 후보 키이어야 함.
제 3정규형을 만족하는 대부분의 릴레이션들은 BCNF도 만족함. 하나의 후보 키만을 가진 릴레이션이 제3 정규형을 만족하면, BCNF도 만족함. BCNF 만드는 방법은 다음과 같다.
- 키가 아니면서 결정자인 애트리뷰트와 그 결정자에 함수적으로 종속하는 애트리뷰트를 하나의 테이블에 넣음. 이 릴레이션에서 결정자는 기본 키가 됨
- 기존 릴레이션에 결정자를 남겨서 기본 키의 구성요소가 되도록 함. 또한 이 결정자는 새로운 릴레이션에 대한 외래 키 역할도 함
7.5. 역정규화(denormalization)
정규화 장점
- 정규화 단계가 진행될수록 중복이 감소하고 갱신 이상도 감소됨
- 무결성 제약조건을 시행하기 위해 필요한 코드의 양도 감소됨
정규화 단점
- 정규화 단계가 진행될수록 하나의 릴레이션이 최소한 두 개의 릴레이션으로 분해됨
- 분해된 릴레이션을 대상으로 질의를 할 때는 정보를 얻기 위해서 보다 많은 릴레이션들을 접근해야 하므로 조인의 필요성이 증가함
많은 데이터베이스 응용에서 검색 질의의 비율이 갱신 질의의 비율보다 훨씬 높음.
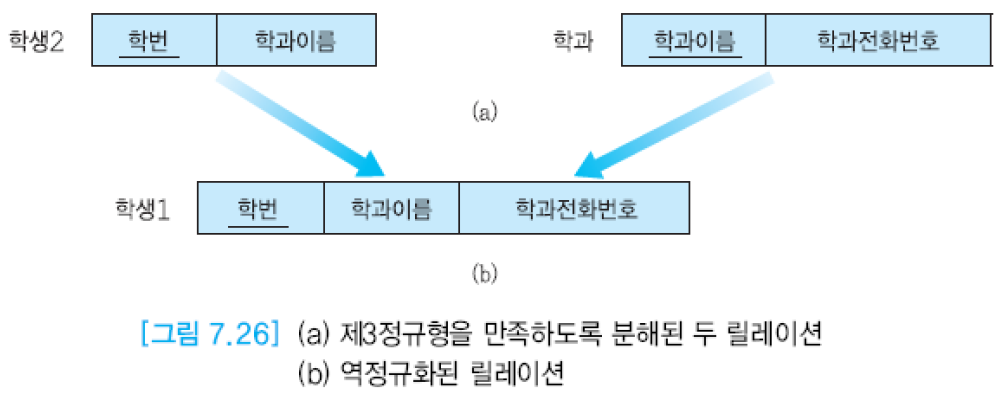
역정규화는 주어진 응용에서 빈번하게 수행되는 검색 질의들의 수행 속도를 높이기 위해서 이미 분해된 두 개 이상의 릴레이션들을 합쳐서 하나의 릴레이션으로 만드는 작업. 즉, 역정규화는 보다 낮은 정규형으로 되돌아가는 것.
댓글남기기